Peculiarities of the conditions of correspondence of biomolecules of higher dimension, necessary for the passage of chemical reactions between them, are considered. As specific examples, the interactions of amino acids with each other and nucleic acids with each other are considered. It is shown that in the case of chemical interaction of biomolecules of higher dimension, the conditions of correspondence (complementarity) are associated with a mirror image of the geometric elements of the corresponding polytopes of higher dimension.

The spatial structure (conformation) of biomolecules plays an extremely important role in many biochemical processes: with the interaction of catalytic centers of enzymes with substrates, when connecting the hormone molecules with its receptor on the surface of the cell, during DNA replication, when transmitting inhuman information and many processes in the cell. Therefore, the study of the spatial structure of biomolecules is an important part of modern studies aimed at clarifying the relationship between the structure of the cells, the structure of their constituent elements and their biochemical functions. To ensure normal biological functions in the interaction of biomolecules, they must sterically accurately correspond to each other (Metzler, 1980; Lehninger, 1985). However, this issue requires additional research. The fact is that recent studies of the structure of biomolecules (Zhizhin, 2016, 2018, 2019, 2021, 2023) show that biomolecules have the highest dimension, i.e. A description of the form of biomolecules in the form of a geometric closed figure leads to a multi -party in the dimension space of more than 3, that is, to a political officer of the highest dimension. In this case, the question of the steric accordance of the interacting biomolecules requires the consideration of the correspondence of biomolecules in the space of the highest dimension. 

At the same time, it cannot be limited to indicating the proximity of the values of some characteristic linear dimensions of the interacting molecules, since the orientation of linear areas in space also plays an important role, especially if this space has the highest dimension. It is not enough to talk about the corresponding of the surfaces of one molecule in relation to another molecule, since the concept of the surface of the molecule in the case of its highest dimension becomes quite uncertain.

In this work, two examples for the biology of living organisms are considered: the interactions of amino acids in the formation of protein and the interaction of nucleic acids in the transmission of hereditary information. From these examples, the extreme importance of taking into account the highest dimension of biomolecules in the analysis of their compounds follows.

Dimensions of protein molecules 

Monomer units which are built of proteins are the 20 standard amino acids. These small molecules containing two different chemical functional groups capable of reacting with each other to form a covalent bond. Amino acids are chemical compounds that simultaneously include a carboxyl group (- COOH) and an amine group (-NH2). These groups are covalently linked to a carbon atom (α - carbon), to which a hydrogen atom H and a side chain R are also covalently attached (Koolman, Roehm, 2013). Connection which determines the formation of protein polymer is called a peptide bond. In the formation of such a connection by joining together - COOH and -NH2 with secretion a molecule of water. Amino acids have two enantiomorphic forms L and D, which are Fischer planar views shown in Figure 1.1. From Figure 1.1 it can be seen that the two enantiomorphic forms are related by mirror image relative to the line passing through the amine and carboxyl groups.

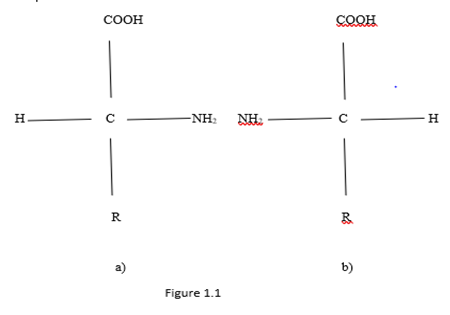
The side chains in Figure 1.1 have 20 variants in classic amino acids (Koolman, Roehm, 2013). They determine the properties of the corresponding amino acids. Fisher's projections do not reflect the spatial structure of amino acids, although it is clear that these are spatial objects. Spatial images of enantiomorphic amino acids (Zhizhin, 2016) are presented in Figure 1.2.

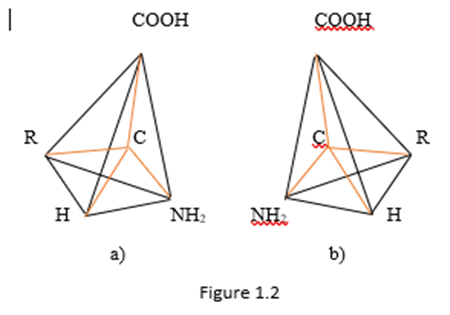
In Figure 1.2, covalent bonds are indicated in red. The rest of the segments define the spatial shape of the molecule, they are marked in black.

From Figure 1.2 it follows that the amino acid molecule is a tetrahedron with a center. The dimension of such a polyhedron can be determined by the Euler - Poincaré equation (Poincaré, 1895)

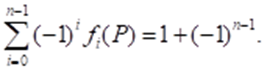
There n is the dimension of a polytope P, which is the number of elements with dimension I in the polytope P.

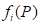
From Figure 1.2 it follows that in any of the two enantiomorphic forms of the amino acid molecule, the number of vertices is 5, the number of edges is 10, the number of two - dimensional faces is 10, the number of three-dimensional faces is 5. In this case

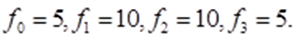
Substituting the obtained values ​​into equation (1), we obtain, 5 – 10 + 10 – 5 = 0.

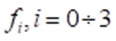
Thus, Euler - Poincaré's equation for a tetrahedron with a center holds for n = 4. This proves that a tetrahedron with a center (amino acid molecule) has dimension 4.

Linear Polypeptide Chain Structure 

The study of diffraction patterns of crystals of amino acids (Pauling, Corey & Branson, 1951; Pauling & Corey, 1950, 1953; Corey & Pauling, 1953) made it possible to establish some values ​​of bond bonds and bond angles in an amino acid. However, the interpretation of the spatial arrangement of atoms in an amino acid requires additional instructions. An example of the possibility of ambiguous interpretation of diffraction patterns can be found in numerous works on the description of quasicrystals. In particular, the apparent icosahedrical symmetry of the diffraction patterns of quasicrystals was proposed to be explained (Pauling, 1987) by multiple twinning of cubic crystals. Pauling based his arguments on the radial arrangement of the spots in the diffractograms. However, high - resolution photomicrographs refuted this assumption (Gratias, Cahn, 1986). The statement about the absence of translational symmetry in quasicrystals (Shechtman, et al., 1984) was constructed using the representations of the three-dimensional geometry of Euclid. Later this statement was refuted (Zhizhin, 2013 a, b; Zhizhin, 2014; Zhizhin, Diudea, 2016). It was proved that translational symmetry in the diffractograms of quasicrystals appears if the diffractograms are considered as projections of structures from the space of higher dimensions. When studying diffraction patterns of amino acid crystals in the works of Pauling joint authors the values ​​of a number of parameters were not determined, for example, bond lengths R – C depending on the species R, bond angles between carbon atoms and nitrogen atoms, between hydrogen atoms and R, etc. To compensate for these disadvantages, it was proposed to use a simplifying assumption about the arrangement of a group of atoms of a peptide bond and centers of tetrahedrons in a plane (Zhizhin, 2020 a, b, c) (Figure 1.3)

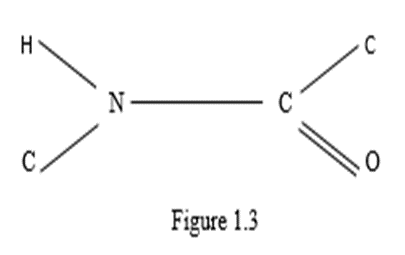
Under this assumption, knowledge of the indicated quantities was not required. It should be noted that in subsequent publications by other authors (Metzler, 1980; Lehninger, 1985; Koolman, Roehm, 2013) with a reference to Pauling's work, it was argued that the arrangement of these atoms in the plane was proved in Pauling's works. But this is not so, to be convinced of this it is enough to refer to these works. This unproven statement became the basis for the construction of three - dimensional models of protein molecules of various conformations in Pauling's works. Let us consider this issue in detail when constructing spatial structures of a linear polypeptide chain. In this case, the atoms of amino acid molecules must be located on a set of parallel lines. Then the polypeptide chain of two molecules of L - amino acids, taking into account the four - dimensionality of amino acid molecules, has the form shown in Figure 1.4.

From Figure 1.4 and Figure 1.5 it can be seen that in order for the corresponding vertices of tetrahedrons with the center (i.e., specific atoms or functional groups) could lie on a system of parallel lines (i.e., form a linear polypeptide chain), it is necessary that the amino acid molecules in the chain alternate with their mirror image relative to the edge in the tetrahedron connecting the bond centers of the polypeptide chain (i.e., relative to the segment CO – NH). The chains in Figure 1.4 and Figure 1.5 differ by the mirror reflection of the molecules relative to the perpendicular to the segment CO – NH (L - and D - molecules).

In the case of a D - amino acid, such a polypeptide chain is shown in Figure 1.5.

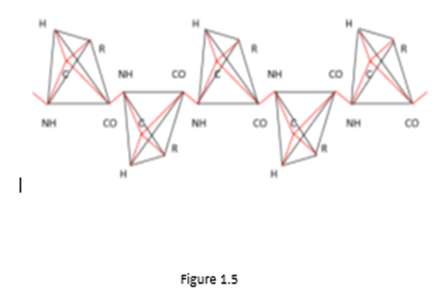
From Figure 1.4 and Figure 1.5 it can be seen that in order for the corresponding vertices of tetrahedrons with the center (i.e., specific atoms or functional groups) could lie on a system of parallel lines (i.e., form a linear polypeptide chain), it is necessary that the amino acid molecules in the chain alternate with their mirror image relative to the edge in the tetrahedron connecting the bond centers of the polypeptide chain (i.e., relative to the segment CO – NH). The chains in Figure 1.4 and Figure 1.5 differ by the mirror reflection of the molecules relative to the perpendicular to the segment CO – NH (L - and D - molecules).

In Figures 1.4 and 1.5, you can see the translational symmetry of the circuits. Moreover, the elementary translational element in this case is a group of two linked amino acid molecules, one of which is a mirror image of another amino acid molecule relative to the segment. From these two linked amino acid molecules, you can create a convex polytope by connecting edges of each vertex of any of the molecules with all other vertices in the group. This is how a simplex polytope of dimension 9 is formed, since the dimension of a simplex polytope is one less than the number of vertices in a simplex (Zhizhin, 2019), and the number of vertices in two tetrahedrons with a center is 10. Therefore, a polypeptide linear amino acid chain has translation symmetry, in which an elementary translation element is a simplex polytope of dimension 9. In Figures 1.4 and 1.5, as well as in Fischer's projections (Figure 1.1) and in spatial images of molecules (Figure 1.2), in accordance with the definition of functional dimension, functional groups R, CO, NH were used. Analysis of Pauling's works on the structure of protein molecules (Pauling, Corey, 1950; Pauling, et al., 1951; Pauling, Corey, 1953; Corey, Pauling, 1953) shows that Pauling's model is nothing more than an assumption. Consider three amino acid residues linked by a peptide bond (Figure 1.6).

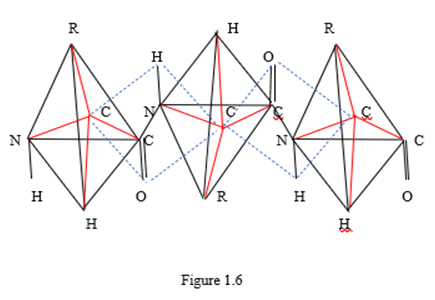
Figure 1.6 shows three amino acid residues in the form of tetrahedra, in the center of which there are three carbon atoms, from which four valence bonds proceed to functional groups located at the vertices of the tetrahedra. These valence bonds are marked with red ribs. Three amino acid residues are linked by two peptide bonds located within two contours, indicated by blue dashed lines. According to Pauling's model, the atoms located on the dotted contour and inside the contour are on the same plane. Here we must take into account that the lengths of chemical bonds connecting different pairs of atoms are different. Calculations of bond angles in Pauling's works are not given for any of the bonds. The plane is determined, as is known, by three points. The statement that some other point belongs to a given plane requires a geometric proof. There is no such evidence in Pauling's work with coworkers. Therefore, Pauling's model remains unproven. From the point of view of chemistry and geometry, the tetrahedral coordination of functional groups relative to the central carbon atom in the amino acid molecule is much more important. This fact should be the basis for the analysis of protein structures.

Thus, it is essential (see Figure 1.6) that the α - carbon atoms do not lie in the same plane with the peptide bond atoms. From a comparison of Figures 1.4 – 1.6 it follows that α - carbon atoms lie either above the plane in which the atoms of the peptide bond are located, or below this plane, and can never lie on this plane. Therefore, Pauling's idea that α - carbon atoms lie in the same plane with functional groups CO, NH is erroneous. Therefore, Pauling's approximation cannot be used both in the construction of linear polypeptide chains and in the construction of more complex conformations of amino acid molecules.

Accounting for the highest dimension of amino acid molecules is also important in the analysis of other possible conformations of protein (spirals, layers, globes). Models of these conformations of the protein are built in the works (Zhizhin, 2020, 2023).

In single - stranded and double - stranded nucleic acids (RNA, DNA), the constituents of acids (residues of phosphoric acid and sugar molecules) interact with each other (Watson, Crick, 1953a, b; Spirin, Gavrilova, 1971; Frank – Kamenetskiy, 1986, 1988). Phosphoric acid residues are connected by divalent metal ions, mainly magnesium ions, due to the interaction of negative charges of phosphoric acid residues with positive charge ions (Spirin, Gavrilova, 1971). This interaction is essential for the stability of nucleic acid structures, especially in the ribosomes. Sugar molecules interact with each other due to the hydrogen bond between the nitrogenous bases attached to the sugar molecules. The constituents of nucleic acids being geometric forms interact with each other to form new geometric forms - new polytopes.  However, it is not known how flat nitrogenous bases are oriented in space, whether their orientation depends on the type of nitrogenous base. Currently, there is no information on this. There is also no information on how exactly the metal ions are located, connecting the phosphoric acid residues. It should be remembered here that the adopted three-dimensional model of the components and the nucleic acid molecule itself is only a model for visual perception. As it was shown earlier, the phosphoric acid residue is a polytope of dimension 4, and the sugar molecule has a dimension of 12. 

The movement of triangles along a helix leads to the formation of polytopes with antiparallel edges. Consider an arbitrary triangle ABC on the plane. Choose some point O/ on the plane outside the triangle to his left. Let this point be the base of the axis of the helix passing through the triangle. Rotate the ABC triangle 180 degrees to the right, moving it up the helix, parallel to the initial plane. In the projection on the plane, both triangles ABC and the displaced triangle ABC will be located as shown in Figure 2.1.

It is easy to see that the edges of the triangle ABC and ABC are antiparallel. It can now connect in space the vertices of the triangle ABC with the vertices of the triangle ABC so that there are no connections of the vertices with the same letters. In a projection on the plane the connections are represented by dotted segments. It can be seen that the connecting segments also break up into pairs of antiparallel segments. Let us now verify that the image ABCA/B/C/ in Figure 2.1, along with the dotted segments, is a projection of a three - dimensional convex polytope. We use the Euler – Poincaré equation (Poincaré, 1895) (1) for this aim.

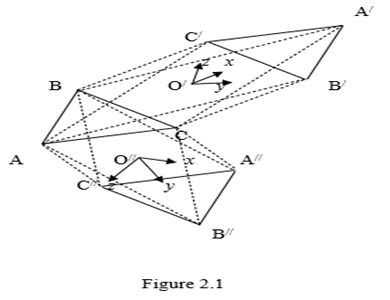
The shape ABCA/B/C/in Figure 2.1 has 6 vertices, 12 edges, 8 triangular faces (rectangles are not faces by construction, since connecting, for example, vertex A with vertices B,C it turns out to be exactly the triangle ABC). Substituting these values of elements of different dimensions into equation (2.1), can find 6 – 12 +8 = 2, i. e. the Euler – Poincaré equation holds in this case for n = 3. This proves that the resulting figure is a convex polytope of dimension 3 (if the figure were not convex, the Euler – Poincaré equation would be violated). The point O/ in Figure 2.1 coincides with the center of the three - dimensional figure ABCA/B/C/ as diagonal figures pass through it and point O/ located on the axis of the helix. Point O/ can be considered as the origin of three - dimensional space. Coordinate axes x, y, z in this direction emanates from directionsA/A/, B/B/, C/C/ respectively. Three pairs of these axes define the coordinate planes of the space of this shape. Choose some point O// on the plane outside the triangle below it. Let this point be the base of the axis of the helix passing through the triangle. Rotate the ABC triangle 180 degrees to the left, moving it up the helix, parallel to the initial plane. In the projection on the plane, both triangles ABC and the displaced triangle A//B//C// will be located as shown in Figure 2.1.

It is easy to see that the edges of the triangle ABC and A//B//C// are antiparallel. It can now connect in space the vertices of the triangle ABC with the vertices of the triangle A//B//C// so that there are no connections of the vertices with the same letters. In a projection on the plane the connection are represented by dotted segments. It can be seen that the connecting segments also break up into pairs of antiparallel segments. Let us now verify that the image ABCA/B/C/in Figure 2.1, along with the dotted segments, is a projection of a three - dimensional convex polytope. Obviously, a shape ABCA//B//C// has as many vertices, edges, and flat faces as a shape ABCA/B/C/. Therefore, it satisfies the Euler – Poincaré equation (1) with dimensionality n = 3, i. e. it is a convex three - dimensional polyhedron. The point O// in Figure 2.1 coincides with the center of the three - dimensional figure ABCA//B//C//as diagonal figures pass through it and point O// located on the axis of the helix. Point O/ can be considered as the origin of three - dimensional space. Coordinate axes x, y, z in this direction emanates from directions AA/, BB/, CC/ respectively. The order of the coordinate axes x, y, z in the figures ABCA/B/C/ and ABCA//B//C//, as can be seen from Figure 2.1, coincide. This suggests that both figures ABCA/B/C/ and ABCA//B//C//are topologically one and same figure - the wrong octahedron.

The Polytope of Hereditary Information

Let us consider in detail the formation of a polytope of two sugar molecules with anti - parallel edges. Here, as in the case of the tetrahedron, to form a polytope with antiparallel edges from two sugar molecules, you must have one sugar molecule on one helix to turn this helix together with the sugar molecule and move the sugar molecule along this reversed helix in opposite direction to the original helix direction. When the sugar molecule rotates 180 degrees to the right while moving, then the original sugar molecule and the sugar molecule on the reversed helix are two polytopes with anti - parallel edges. Both of these sugar molecules in a simplified form are represented in Figure 2.2.

When the five - carbon sugar molecule is rotated to the left by 180 degrees, the nitrogenous bases are on opposite sides of both molecules, so that for their connection it is necessary to cross the entire set of atoms of two molecules. This is unrealistic therefore this option is not considered. When the sugar molecule is rotated 180 degrees to the left, it is possible to connect the sugar molecules through nitrogenous bases only between two different chains of nucleic acids or in the case of turning the chain itself in the opposite direction.

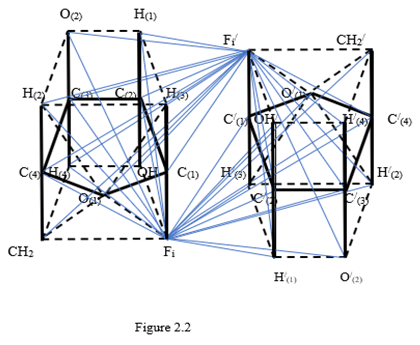
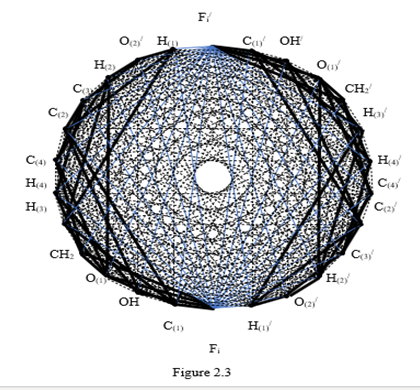
In full, the sugar molecules have a dimension of 12, in the corresponding polytope each vertex must have an edge connection with all the other vertices. Knowledge of this now one need. For the formation of a polytope of dimension 13, it is necessary to connect each vertex of one polytope with the vertices of another polytope so that there are no vertex connections with the same letters. All connecting edges break into pairs of antiparallel edges. At the same time, a set of coordinate a two - dimensional planes emanates from the center of the formed polytope as from the origin of coordinates. Their number is equal to the number of combinations from 13 to 2, i. e. 48 coordinate planes. In order to clarify the possible geometrical circumstances of the connection of helices in double - helix nucleic acid molecules with nitrogenous bases, we are primarily interested in the coordinate planes containing these nitrogenous bases. There are exactly 12 such coordinate planes in the obtained polytope of dimension 13. They are depicted in Figure 2.3 by blue solid lines and are indicated below by the vertices of the polytopes contained in them

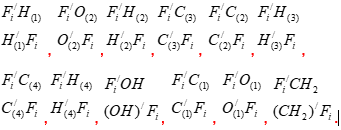
Other edges of the polytope of dimension 13 are not shown in Figure 2.2, so as not to ignite the figure. In the center of each parallelogram, indicated by its four vertices, is the origin of coordinates and the corresponding pair of coordinate axes (they are not shown). To identify the different hydrogen and oxygen atoms at vertices of polytope, they indicated by numbers in brackets at the lower indices.

It is surprising that the number of coordinate planes containing vertices is exactly equal to the number of possible compounds of nitrogenous bases 12 (Spirin, 2019)

Since each coordinate plane designated by the vertices of the parallelograms has a specific atomic environment, it can be assumed that each of the 12 possible compounds of nitrogenous bases is located on one particular coordinate plane out of 12 possible. This solves the question of the possible orientation of the bond of nitrogenous flat bases in nucleic acids using ideas about the high dimensionality of the constituent nucleic acids. It is also surprising that in order to create 13 – cross - polytopes, providing the connection with nitrogenous bases, nature specially created double - stranded nucleic acids with oppositely directed spirals. This is realized in DNA and RNA when creating regions with inverted helices. 

In a variety of nucleic acid molecules, the issue of chain interaction is important. In ribosomes, RNA interacts with each other due to bivalent metal ions (mainly magnesium ions). Positively charged magnesium ions attract negative charges of phosphoric acid residues, ensuring the stability of the ribosomes. In double - stranded nucleic acids, the helices are connected to each other by means of nitrogenous bases complementarily interacting with each other by a hydrogen bond. However, the magnesium ions and nitrogen bases in nucleic acids could not be specifically located. It has been established that magnesium ions and flat nitrogenous bases can be located inside special polytopes of higher dimension. Here knowledge is needed of the higher dimension of phosphoric acid residues and sugar molecules. Such polytopes are polytopes with anti - parallel edges, i.e., cross - polytopes of higher dimension. Binding agents are located on the free coordinate planes of these polytopes in the vicinity the center of the polytope. 

In this case, the two - dimensional coordinate plane on the boundary of the polytope should contain the objects to be joined. In the case of magnesium ions, there are four specific coordinate planes inside the 5 – cross - polytope, in which an ion can accommodate, combining negative charges. In the case of nitrogenous bases, the existence of 12 coordinate planes inside a cross - polytope of dimension 13, in which flat nitrogenous bases can be located, connecting the helix of nucleic acids, was discovered. Exactly as much as there are options for combining nitrogenous bases. It is given, that each coordinate plane of these 12 planes has a specific environment of atoms. It should be assumed that only one of the 12 possible compounds of nitrogenous bases is placed in each of these planes. It is surprising that the existence of higher - dimensional polytopes with anti - parallel edges is possible only in the case of the opposite direction of interacting helices, and this is exactly what nature provides in the double - helix DNA and in the RNA segments with self - inversion of the helix in the opposite direction.

To build the polytopic of hereditary information, we need to supplement Figure 2.2 with edges that create a closed and convex figure. In this case, it is not necessary to connect the vertices symmetrically relative to the center of Figure 2.2 with the edges. Each vertex will be connected by an edge to the other vertices. In this case, the polytope will be a cross - polytope and its dimension is equal to half the number of vertices. Indeed, according to (Zhizhin, 2019 a), there is a relation between the number of dimension elements i in the cross - polytope and the dimension d of the cross - polytope itself,

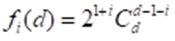
At the vertex i = 0, therefore, according to (2) 

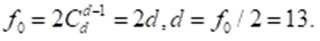
Thus, the polytope of the hereditary information has dimension 13. When portraying this polytope, we will use the technique that is used in portraying cross - polytopes. We distribute all 26 vertices on the circle so that the vertices opposite in Figure 2.2 remain opposite and there is no edge between them (Figure 2.3). 

The edges corresponding to the chemical bonds are indicated in this figure by thick black solid lines. Anti-parallel edges highlighting coordinate planes with vertices corresponding to nitrogenous bases are indicated by bluey lines. The remaining edges are indicated by thin dash-dotted black lines. We emphasize that there is a chemical bond between the nitrogenous bases, but it is not covalent. Therefore, this connection is not indicated by an edge.

When the polytope of hereditary information moves along the common axis of the double helix of nucleic acids in accordance with the sequence of bases in DNA, the connection between the vertices is carried out by one of the twelve base pairs, which occupies one of the 12 coordinate planes of the polytope.

The Law of Conservation of Incidents in Polytope of Hereditary Information

The monograph (Zhizhin, 2019) introduced the concept of the incidence coefficients of elements of lower dimension with respect to elements of the higher dimension and elements of higher dimension with respect to elements of the lower dimension. The first characterizes the number of elements of a certain higher dimension to which the given element of a lower dimension belongs. The second characterizes the number of elements of a given lower dimension that are included in a particular element of a higher dimension. Here we must remember that the vertices of geometric elements of various dimensions are atoms, molecules or functional groups. Therefore, the incidence of geometric elements to a friend means contact between particles of the matter, including living matter. The contact between particles of matter can be interpreted as the transfer of information on material structures, including biological structures. It was proved that the sum of incidents retains its value when changes the direction of the relationship between the elements (the law of conservation of incidents) (Zhizhin, 2019). For the polytope of hereditary information this value is 1.78 109. A significant value of the total incidence stream in the polytope of hereditary information indicates an intensive exchange of information between elements of the polytope of hereditary information. This may explain for the recently discovered epigenetic principle of the transmission of hereditary information without changing the sequence of genes in DNA and RNA molecules (Hawkes, et al, 2016; Lindquist, et al., 2016; Mancuso, 2017).

The studies carried out show that with a large dimension of interacting biomolecules, the condition for their correspondence (complementarity) can only be the condition that ensures the possibility of a chemical reaction between molecules. Moreover, since the molecules have a higher dimension, i.e. are representable as polytopes of higher dimension, then only the condition of correspondence to the geometry of polytopes of higher dimension can be a correspondence condition. In the examples considered, this correspondence condition is associated with a mirror image of the geometric elements of one polytope in relation to the geometric elements of the polytope interacting with it. So, when considering the formation of a chain of polytopes along a line (the interaction of amino acid molecules), the bound molecules turned out to be mirror images of each other relative to the line along which they line up. During the interaction of nucleic acids, the interacting sugar molecules are also connected by mirror reflection, forming polytopes with antiparallel edges, i.e., high-dimensional cross-polytopes.