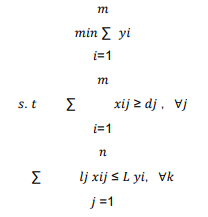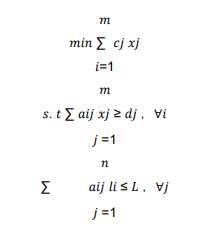Review Article | DOI: https://doi.org/10.58489/2836-2330/012
Mathematical analysis on troubleshooting problem during COVID-19 pandemic
- School of Science, Hubei University of Technology, Wuhan, Hubei, China.
- Hospital, Hubei University of Technology, Wuhan, Hubei, China.
*Corresponding Author: Bin Zhao
Citation: Bin Zhao, Xia Jiang (2023). Mathematical analysis on troubleshooting problem during COVID-19 pandemic. Journal of Clinical and Medical Reviews. 2(1). DOI: 10.58489/2836-2330/012.
Copyright: © 2023 Bin Zhao, this is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received: 09 November 2022 | Accepted: 25 November 2022 | Published: 02 March 2023
Keywords: Nesting, mathematical models, troubleshooting problem
Abstract
Mathematics is closely related to people's daily lives, such as the various shapes that can be seen everywhere, and the various distance relationships. Similarly, industrial production is inseparable from mathematics. The problem of nesting is a representative planning problem in industry and is widely used in the fields of construction, clothing, machinery and wood. With the development of computers, the nesting problem has been significantly improved by relying on the emergence of some intelligent algorithms. However, at the beginning of the problem, establishing a reasonable mathematical model is an essential step. This article summarizes thecommon mathematical models in the troubleshooting problem and analyzesthe advantages and disadvantages during COVID-19 pandemic.
Introduction
The nesting problem, also known as the unloading problem. It refers to the slitting out of a variety of parts of differentlengths from a specification of the materialto maximize the utilization rate of the material. According to the dimensionality of raw materials, nesting problems can be classified into the followingcategories: one-dimensional blankingproblems, two-dimensional blankingproblems, and three-dimensional blanking problems during COVID-19 pandemic.
Depending on the type of part, one dimensional nesting problems can be divided into one-dimensional nesting problems with a single specification (the length of raw materials are equal) and one-dimensional nesting problems with multiple specifications (different lengths of raw materials).
According to the quantity of raw materials, it can be divided into complete unloading (the quantity of raw materials is sufficient to obtain all required profiles)and incomplete unloading(the number of raw materials is limited, only part of the demand profiles can be obtained) problems. The one-dimensional blanking problem belongs to the NP problem, the number of solutions is incalculable, and it cannot be solved using a simple exhaustive method, so some accurate mathematical models are needed to describe it.
Mathematical models
In the nesting problem, some mathematical models are often needed to represent the solution results, and the quality of the model is related to the quality of the results. This section describes two common mathematical models.
1.Kantorovichmodel [1]
where: m is the total number of raw material roots of the unloading, i is the serial number of the raw material,i = 1, 2, 3, m, n is the number of parts to be unloaded,
j is the serial number of the part, j = 1,2, 3, n,lj is the length of the part j, dj is the
demand quantity of the part j, L is the length of the raw material, xij is the number of cutting roots of the first part in the i-root raw material, yi is the variable 0-1, if the i-root raw material is used for the blanking, then yi = 1, otherwise yi = 0.
2.Gilmore-Gomorymodel [2]
where: i is the part serial number, i = 1, 2,3, ......, n, j is the unloading mode serial number, j = 1,2, 3, m, and cj is the cost of using the jth unloading mode; aij is the
number of cuts in the part i in the unloading mode j; xj is the number of raw materials requiredto use the j-type unloadingmode.
Analyse
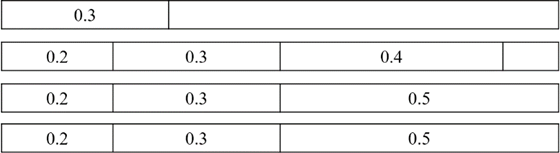
There are the following examples: there are 1 m long raw materials, now need to get 0.2 m long 3, 0.3 m long 4, 0.4 m long 1, 0.5 m long 2, how to cut the most economical material. In the second section, two mathematical models are introduced. The objective function of the Kantorovich model is the total number of roots consumed by the raw material, and the decision function is that the number of parts of a single kind needs to be greater than the number of demanded parts, and the length of
each raw material needs to be greater than all the parts obtained from the raw material. Using the results of the model, two results may appear as shown in Figure 1, Figure 2, wherein the first way is 0.2 m, 0.3 m, 0.5 m for a group, cut two, 0.3 m, 0.3 m, 0.4 m for a group, cut one, 0.2 m for a group, cut one; The second way is 0.2 m, 0.3 m, 0.5 m for a group, cut two, 0.2 m, 0.3 m, 0.4 m for a group, cut one, 0.3 m for a group, cut one. Comparing the two methods, both meet the Kantorovich model, but the utilization rate obtained at this time is obviously different [3, 12].
In the Gilmore-Gomory model, there is a m-seed unloading pattern,where the objective function is the scrap rate of raw materials, and the decision function is consistent with the Kantorovich model. For the Gilmore-Gomory model, the problem on the Kantorovich model was solved to some extent, but it would undoubtedly cost more time before waiting for the results.
Comparing the two models, the Kantorovich model solves the time cost, while the Gilmore-Gomory model saves materials, and the choice of the two modes should be combined with the production reality, balancing the relationship between time and material [12, 19].
Summary
Mathematical thought refers to the spatial form and quantitative relationship of the real world reflected in human consciousness, through the thinking activities and produce a result, it is the basic view of dealing with problems in mathematics, is a summary of the basic knowledge of mathematics and the essence of basic methods, is the guideline for the creative development of mathematics [20, 26]. Through the cultivation of mathematical ideas, the ability of mathematics will be greatly improved. To master mathematical ideas is to master the essence of mathematics. For mathematics, the ultimate goal must be to combine it with reality, and mathematics divorced from reality is meaningless. In industry, mathematics is often linked to increasing the number of productivities, utilization, etc., and to improve these values, more accurate mathematical models are needed, so our learning of mathematics should be more in-depth and not stagnant [27, 33].
Conflict of interest
We have no conflict of interests to disclose and the manuscript has been read and approved by all named authors.
Acknowledgments
Thiswork was supportedby the Philosophical and Social Sciences ResearchProject of Hubei Education Department (19Y049), and the Staring ResearchFoundation for the Ph.D. of Hubei University of Technology (BSQD2019054), Hubei Province, China.
References
- L. V. Kantorovich. (1960). Mathematical Methods of Organizing and Planning Production. Management Science, 6(4): 366–422.
View at Publisher | View at Google Scholar - Gilmore P C., & Gomory R E. (1961). A linear programming approach to the cutting stock problem. Operations Research, 9(2): 849–859.
View at Publisher | View at Google Scholar - Babu, A. R., & Babu, N. R. (2001). A generic approach for nesting of 2-D parts in 2-D sheets using genetic and heuristic algorithms. Computer-Aided Design, 33(12), 879–891.
View at Publisher | View at Google Scholar - Baker, B. S., Coffman, E. G., & Rivest, R. L. (1980). Orthogonal packings in two dimensions. SIAM Journal on Computing, 9(4), 846–855.
View at Publisher | View at Google Scholar - Baldacci, R., Boschetti, M. A., Ganovelli, M., & Maniezzo, V. (2014). Algorithms for nesting with defects. Discrete Applied Mathematics, 163, 17–33.
View at Publisher | View at Google Scholar - Bengio, Y., Lodi, A., & Prouvost, A. (2021). Machine learning for combinatorial optimization: a methodological tour d’horizon. European Journal of Operational Research, 290(2), 405–421.
View at Publisher | View at Google Scholar - Bennell, J. A., & Oliveira, J. F. (2008). The geometry of nesting problems: A tutorial. European Journal of Operational Research, 184(2), 397–415.
View at Publisher | View at Google Scholar - Cherri, L. H., Cherri, A. C., & Soler, E. M. (2018). Mixed integer quadraticallyconstrained programming model to solve the irregular strip packing problem with continuous rotations. Journal of Global Optimization, 72(1), 89–107.
View at Publisher | View at Google Scholar - Cherri, L. H., Mundim, L. R., Andretta, M., Toledo, F. M., Oliveira, J. F., & Carravilla, M. A. (2016). Robust mixed-integer linear programming models for the irregular strip packing problem. European Journal of Operational Research, 253(3), 570–583.
View at Publisher | View at Google Scholar - Chryssolouris, G., Papakostas, N., & Mourtzis, D. (2000). A decision-making approach for nesting scheduling: a textile case. International Journal of Productions Research, 38(17), 4555–4564.
View at Publisher | View at Google Scholar - Dowsland, K. A., Vaid, S., & Dowsland, W. B. (2002). An algorithm for polygon placement using a bottom-left strategy. European Journal of Operational Research, 141(2), 371–381.
View at Publisher | View at Google Scholar - Elkeran, A. (2013). A new approach for sheet nesting problem using guided cuckoo search and pairwise clustering. European Journal of Operational Research, 231(3), 757–769.
View at Publisher | View at Google Scholar - Gahm, C., Uzunoglu, A., Wahl, S., Ganschinietz, C., & Tuma, A. (2022). Applying machine learning for the anticipation of complex nesting solutions in hierarchical production planning. European Journal of Operational Research, 296(3), 819–836.
View at Publisher | View at Google Scholar - Leao, A. A., Toledo, F. M., Oliveira, J. F., Carravilla, M. A., & Alvarez-Valdés, R. (2020). Irregular packing problems: A review of mathematical models. European Journal of Operational Research, 282(3), 803–822.
View at Publisher | View at Google Scholar - Pinheiro, P. R., Júnior, B. A., & Saraiva, R. D. (2016). A random -key genetic algorithm for solving the nesting problem. International Journal of Computer Integrated Manufacturing, 29(11), 1159–1165.
View at Publisher | View at Google Scholar - Plisnier, H., Steckelmacher, D., Roijers, D. M., & Nowé, A. (2019). Transfer reinforcement learning across environment dynamics with multiple advisors. In BNAIC/BENELEARN. Rakotonirainy, R. G. (2020). A machine learning approach for automated strip packing algorithm selection. ORiON, 36(2), 73–88.
View at Publisher | View at Google Scholar - Sato, A. K., Martins, T. C., Gomes, A. M., & Tsuzuki, M. S. G. (2019). Raster penetration map applied to the irregular packing problem. European Journal of Operational Research, 279(2), 657–671.
View at Publisher | View at Google Scholar - Sutton, R. S., & Barto, A. G. (2018). Reinforcement learning: an introduction. MIT Press. Toledo,
View at Publisher | View at Google Scholar - Akunuru, R., & Babu, N. (2013). Semi-discrete geometric representation for nesting problems. International Journal of Production Research, 51, 4155–4174.
View at Publisher | View at Google Scholar - Baldacci, R., Boschetti, M., Ganovelli, M., & Maniezzo, V. (2014). Algorithms for nesting with defects. Discrete Applied Mathematics, 163, 17–33.
View at Publisher | View at Google Scholar - Bennell, J., & Oliveira, J. (2008). The geometry of nesting problem: A tutorial. European Journal of Operational Research, 184, 397–415.
View at Publisher | View at Google Scholar - Burke, E., Hellier, R., Kendall, G., & Whitwell, G. (2010). Irregular packing using the line and arc no-fit polygon. Operations Research, 58, 948–970.
View at Publisher | View at Google Scholar - Cherri, L., Carravilla, M., & Toledo, F. (2016). A model-based heuristic for the irregular strip packing problem. Pesquisa Operacional, 36, 447–468.
View at Publisher | View at Google Scholar - Gomes, A. M. (2013). Irregular packing problems: Industrial applications and new directions using computational geometry. IFAC-Proceedings, 46, 378–383.
View at Publisher | View at Google Scholar - Gomes, A. M., & Oliveira, J. (2002). A 2-exchange heuristic for nesting problems.European Journal of Operational Research, 141, 359–370.
View at Publisher | View at Google Scholar - Kierkosz, I., & Luczak, M. (2019). A one-pass nesting problems. Operations Research and Decisions, 29, 37–60.
View at Publisher | View at Google Scholar - Leao, A., Toledo, F., Oliveira, J., & Carravilla, M. (2015). A semi-continuous MIP model for the irregular strip packing problem. International Journal of Production Research, 54, 712–721
View at Publisher | View at Google Scholar - Leao, A., Toledo, F., Oliveira, J., Carravilla, M., & Alvarez-Valds, R. (2020). Irregular packing problems: A review of mathematical models. European Journal of Operational Research, 282, 803–822.
View at Publisher | View at Google Scholar - Pinheiro, P. R., Amaro Junior, B., & Saraiva, R. D. (2016). A random-key genetic algorithm for solving the nesting problem. International Journal of Computer Integrated Manufacturing, 29, 1159–1165.
View at Publisher | View at Google Scholar - Sato, A., Martins, T., Gomes, A., & Tsuzuki, M. (2019). Raster penetration map applied to the irregular packing problem. European Journal of Operational Research, 279, 657–671.
View at Publisher | View at Google Scholar - Sato, A., Martins, T., & Tsuzuki, M. (2016a). A pairwise exact placement algorithm for the irregular nesting problem. International Journal of Computer Integrated Manufacturing, 29, 1177–1189.
View at Publisher | View at Google Scholar - Sato, A. K., Tsuzuki, M. S. G., Martins, T. C., & Gomes, A. M. (2016b). Study of the grid size impact on a raster-based strip packing problem solution. IFAC-Papers on Line, 49, 143–148.
View at Publisher | View at Google Scholar - Toledo, F., Carravilla, M., Ribeiro, C., Oliveira, J., & Gomes, A. M. (2013). The dotted-board model: A new MIP model for nesting irregular shapes. International Journal of Production Economics, 145, 478–487.
View at Publisher | View at Google Scholar